2 Answers

Tiago Peres · Answer 1 · 2021-06-12T07:44:01+0000

Given:

Given that the radius of the circle is 2 inches.

We need to determine the area of the remaining square.

Area of a square:

Given that each circle has a radius of 2 inches.

Then, the diameter of each circle is 4 inches.

Hence, the side length of the square is 2 × 4 = 8 inches.

The area of the square is given by

A=s^2

A=8^2

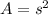
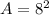
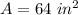
$A=64 \ in^2$

Thus, the area of the square is 64 square inches.

Area of the four circles:

The area of one circle is given by

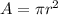
$A=\pi r^2$

Substituting r = 2, we have;

$A=4 \pi$

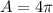
Thus, the area of one circle is 4π in²

The area of 4 circles is 4 × 4π =16π in²

Hence, the area of the 4 circles is 16π in²

Area of the remaining square:

The area of the remaining square is given by

Area = Area of the square - Area of four circles.

Substituting the values, we get;

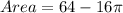
$Area = 64-16 \pi$

Thus, the area of the remaining square is (64 - 16π) in²

Hence, Option c is the correct answer.

Please log in or register to add a comment.