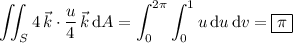Stokes' theorem says the integral of the curl of
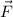 over a surface
over a surface
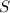 with boundary
with boundary
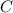 is equal to the integral of
is equal to the integral of
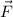 along the boundary. In other words, the flux of the curl of the vector field is equal to the circulation of the field, such that
along the boundary. In other words, the flux of the curl of the vector field is equal to the circulation of the field, such that
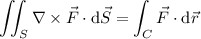
We have
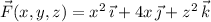
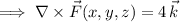
Parameterize the ellipse
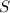 by
by
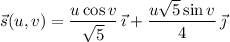
with
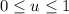 and
and
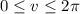 .
.
Take the normal vector to
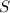 to be
to be
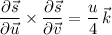
Then the flux of the curl is