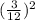Answer:
The options b) ,c) and e) are correct
The three choices shows the ratio of the area of the smaller rectangle to the area of the larger rectangle are b)
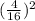 , c)
, c)
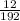 and e)
and e)
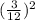
Explanation:
Given that a large rectangle has a length of 16 and width of 12.
A smaller rectangle has length of 4 and width of 3
To show the ratio of the area of the smaller rectangle to the area of the larger rectangle:
we know that "If two figures are similar, the the ratio of its areas is equal to the scale factor squared"
From the given scale factor is
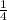
Let z be the scale factor
Let x be the area of the smaller rectangle
Let y be the area of the large rectangle
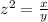
Since scale factor is
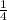 hence
hence
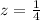
we have
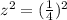
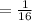
∴
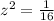
Now show that the ratio of the area of the smaller rectangle to the area of the larger rectangle with each options.
a)
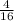
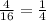
Compare with
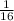 we get,
we get,
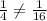
Hence it is not possible.
b)
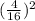
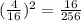
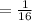
Compare with
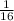 we get,
we get,
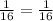
This implies that the ratio of the area of the smaller rectangle to the area of the larger rectangle.
c)
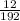
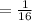
Compare with
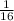 we get,
we get,
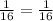
This implies that the ratio of the area of the smaller rectangle to the area of the larger rectangle.
d)
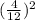
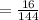
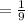
Compare with
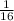 we get,
we get,
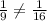
Hence it is not possible.
e)
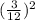
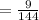
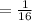
Compare with
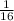 we get,
we get,
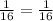
This implies that the ratio of the area of the smaller rectangle to the area of the larger rectangle.
∴ options b) ,c) and e) are correct
The three choices shows the ratio of the area of the smaller rectangle to the area of the larger rectangle are b)
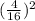 , c)
, c)
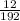 and e)
and e)