Question

One hundred tickets, numbered 1, 2, 3, . . . , 100, are sold to 100 different people for a drawing. Four different prizes are awarded, including a grand prize (a trip to Tahiti). How many ways are there to award the prizes if it satisfies the given conditions.

Answer 1

The number of ways to award the prizes if it satisfies the given conditions is 94,109,400.

Explanation:

There are 100 tickets that are distributed among 100 different people.

Four different prizes are awarded, including a grand prize.

The selection of the four wining tickets can be done using permutations.

Permutation is an arrangement of all the data set in a specific order.

The formula to compute the permutation of k objects from n different objects is:

`^(n)P_(k)=(n!)/((n-k)!)`

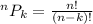
In this case we need to compute the number of selection of the 4 winning tickets accordingly from 100 tickets.

Compute the number of ways to select 4 winning tickets as follows:

`^(n)P_(k)=(n!)/((n-k)!)`

`^(100)P_(4)=(100!)/((100-4)!)`

`=(100!)/(96!)`

`=(100*99*98*97*96!)/(96!)`

`=94109400`

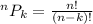
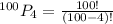
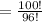
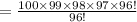
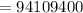
Thus, the number of ways to award the prizes if it satisfies the given conditions is 94,109,400.