Use the discriminate to determine how many solutions this equation has -8x^2-8x-2=0

Question

asked Apr 20, 2023 48.3k views

2 Answers

Gianpi · Answer 1 · 2023-04-26T08:59:34+0000

Answer:

One solution

Explanation:

Discriminant

$\textsf{Discriminant}:b^2-4ac}\quad\textsf{when}\:ax^2+bx+c=0$

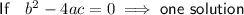
$\textsf{If}\quad b^2-4ac=0 \implies \textsf{one solution}$

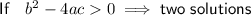
$\textsf{If}\quad b^2-4ac > 0 \implies \textsf{two solutions}$

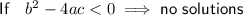
$\textsf{If}\quad b^2-4ac < 0 \implies \textsf{no solutions}$

Given equation:

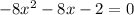
-8x^2-8x-2=0

Swap sides:

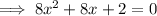
$\implies 8x^2+8x+2=0$

Using discriminant:

$\implies b^2-4ac=8^2-4(8)(2)=0$

Therefore, there is one solution

--------------------------------------------------------------------------------------------

Proof

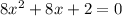
8x^2+8x+2=0

Divide both sides by 2:

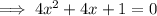
$\implies 4x^2+4x+1=0$

Separate the middle term:

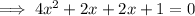
$\implies 4x^2+2x+2x+1=0$

Factor the first two terms and the last two terms separately:

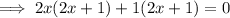
$\implies 2x(2x+1)+1(2x+1)=0$

Factor out the common term
(2x+1) :

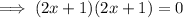
$\implies (2x+1)(2x+1)=0$

Therefore:

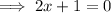
$\implies 2x+1=0$

$\implies x=-\frac12$

Thus proving there is one solution.