Question

Sarah’s stands on a ground and sights the top of a steep Clift at a 60 degree angle of elevation she then steps back 50 meters then sights the top of the steep cliff at a 30 degree angle if Sarah is 1.8 meters tall how tall is the cliff to the nearest meter ?

Answer 1

Cliff is 45 m tall.

Explanation:

Given:

Height of Sarah = 1.8 m

Angle of elevation = 60°

Angle of elevation 50 m back = 30°

As shown in the figure we have two right angled triangles SPQ and SPR.

Let the height of the cliff be
`h` meters and
`h= h_1+h_s`.

Using trigonometric ratios:

tan (Ф) = opposite/adjacent

In ΔSPQ. In ΔSPR.

⇒
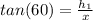`tan(60) = (h_1)/(x)` ...equation (i) ⇒
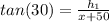`tan (30)=(h_1)/(x+50)` ...equation (ii)

Dividing equation (i) and (ii)

⇒
`(tan(60))/(tan(30)) = (h_1)/(x) * (x+50)/(h_1)`

⇒
`3 = (x+50)/(x)`

⇒
`3x=x+50`

⇒
`3x-x=50`

⇒
`2x=50`

⇒
`x=(50)/(2)`

⇒
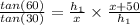
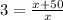
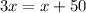
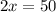
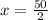
`x=25` meters

To find
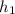`h_1` plugging
`x=25` in equation (i)

⇒
`h_1=x* tan(60)`

⇒
`h_1=25* 1.73`

⇒
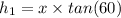
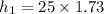
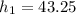`h_1=43.25` meters

The height of the cliff from ground :

⇒
`h= h_1+h_s`

⇒
`h= 43.25+1.8`

⇒
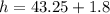
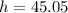`h=45.05` meters

The cliff is 45 m tall to the nearest meter.