Question

Help with all questions in pictures please

Just put the answers please (ex: 1A 2C 3B. etc)
For question number 7 where it says (Which of the following images represents the polar graph of r = 4cos 2θ?) only two of the graphs are shown please if you can include a graph of the correct answer *70Points*

Answer 1

See below for answers and explanations

Explanation:

Problem 1

Convert point Q to polar coordinates (accounting for correct direction):

`\displaystyle r=√(x^2+y^2)=\sqrt{(-5)^2+(-5√(3))^2}=√(25+75)=√(100)=10\\\\\theta=\tan^(-1)\biggr((-5√(3))/(-5)\biggr)=\tan^(-1)\bigr(√(3)\bigr)=(4\pi)/(3)`

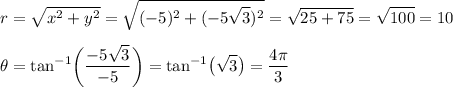
Thus, the answer is
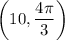`\displaystyle \biggr(10,(4\pi)/(3)\biggr)`, or A

Problem 2

Make polar substitutions:

`x^2+y^2-2x+8y=0\\\\r^2-2r\cos\theta+8r\sin\theta=0\\\\r^2=2r\cos\theta-8r\sin\theta\\\\r=2\cos\theta-8\sin\theta\\\\r=-8\sin\theta+2\cos\theta`

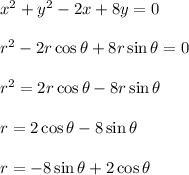
Hence, the answer is C

Problem 3

Eliminate the parameter:

`x=t+3\\x-3=t\\\\y=t^2+2t\\y=(x-3)^2+2(x-3)\\y=x^2-6x+9+2x-6\\y=x^2-4x+3`

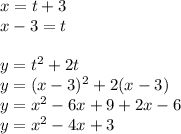
Hence, the answer is C

Problem 4

Identify
`z_1` and
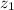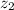`z_2` and add the complex numbers:

`z_1+z_2=(-3+5i)+(-5-2i)=-3+5i-5-2i=-8+3i`

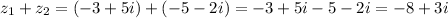
Thus, the correct answer is S

Problem 5

Use the formula for multiplying complex numbers in polar form:

`z_1z_2=r_1r_2(\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2))\\z_1z_2=(5)(15)(\cos(240^\circ+135^\circ)+i\sin(240^\circ+135^\circ))\\z_1z_2=75(\cos375^\circ+i\sin375^\circ)\\z_1z_2=75(\cos15^\circ+i\sin15^\circ)`

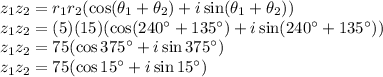
Hence, the answer is A

Problem 6

Determine when the ball first hits the ground:

`y=-(1)/(2)gt^2+(v\sin\theta)t+y_0\\0=-(1)/(2)(32)t^2+(58\sin19^\circ)t+1.9\\0=-16t^2+(58\sin19^\circ)t+1.9\\t\approx1.273`

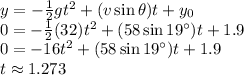
Determine the horizontal distance covered by the ball:

`x=(v\cos\theta)t\\x=(58\cos19^\circ)(1.273)\\x\approx69.811`

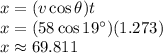
Hence, the best answer is C

Problem 7

The equation is in the form of
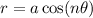`r=a\cos(n\theta)` where
`a` is the length of each petal and the curve has a horizontal pole. If
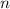`n` is odd, then there are
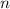`n` petals, but if
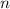`n` is even, then there are
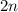`2n` petals.

From our given equation, there are clearly 4 petals since
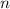`n` is even, and each petal length is 4 units. Hence, the first graph is correct.