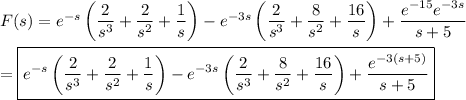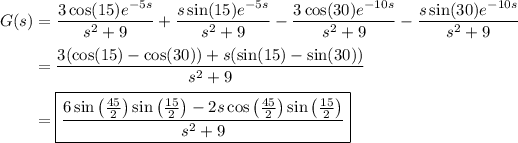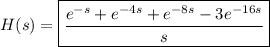Question

Question 1a:

Compute the Laplace Transforms of

f(x) = { x² +2x +1 , x < 3
{ e⁻⁵ˣ , x ≥ 3


​

Answer 1

This is made easy if you know the Laplace transform pair

`u(t - c) y(t - c) \mapsto e^(-cs) Y(s)`

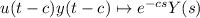
where u(t) is the Heaviside step function and Y(s) is the Laplace transform of y(t).

We rewrite f, g, and h in terms of u :

`f(x) = (x^2+2x+1) (u(x) - u(x-3)) + e^(-5x) u(x-3)`

`g(x) = \sin(3x) (u(x-5) - u(x-10))`

`h(x) = (u(x) - u(x-4)) + 2(u(x-4)-u(x-8)) + 3 (u(x-8)-u(x-16))`

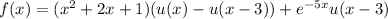
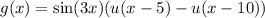
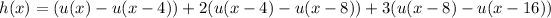
and we also rearrange terms to get the right shift in argument:

`f(x) = (x^2+2x+1) u(x) - ((x-3)^2+8(x-3)+16) u(x-3) + e^(-15) e^(-5(x-3)) u(x-3)`

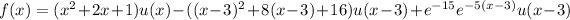
`g(x) = [\cos(15) \sin(3(x-5)) + \sin(15) \cos(3(x-5))] u(x-5) \\\\ ~~~~~~~~~~- [\cos(30) \sin(3(x-10)) + \sin(30) \cos(3(x-10))] u(x - 10)`

`h(x) = u(x) + u(x-4) + u(x-8) - 3 u(x - 16)`

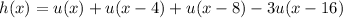
Now we can apply the known transform pair, along with

`x^n \mapsto (n!)/(s^(n+1))`

`e^(ax) \mapsto \frac1{s-a}`

`\sin(ax) \mapsto (a)/(s^2+a^2)`

`\cos(ax) \mapsto (s)/(s^2+a^2)`

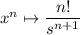
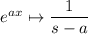
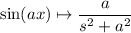
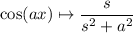
The transforms of f, g, and h are then

`F(s) = e^(-s) \left(\frac2{s^3} + \frac2{s^2} + \frac1s\right) - e^(-3s) \left(\frac2{s^3} + \frac8{s^2} + \frac{16}s\right) + (e^(-15) e^(-3s))/(s + 5) \\\\ = \boxed{e^(-s) \left(\frac2{s^3} + \frac2{s^2} + \frac1s\right) - e^(-3s) \left(\frac2{s^3} + \frac8{s^2} + \frac{16}s\right) + (e^(-3(s+5)))/(s + 5)}`

`G(s) = (3\cos(15) e^(-5s))/(s^2+9) + (s \sin(15) e^(-5s))/(s^2+9) - (3\cos(30)e^(-10s))/(s^2+9) - (s \sin(30) e^(-10s))/(s^2+9) \\\\ ~~~~~~~ = (3(\cos(15)-\cos(30)) + s(\sin(15) - \sin(30)))/(s^2+9) \\\\ ~~~~~~~ = \boxed{\frac{6\sin\left(\frac{45}2\right)\sin\left(\frac{15}2\right) - 2s \cos\left(\frac{45}2\right)\sin\left(\frac{15}2\right)}{s^2+9}}`

`H(s) = \boxed{\frac{e^(-s) + e^(-4s) + e^(-8s) - 3 e^(-16s)}s}`