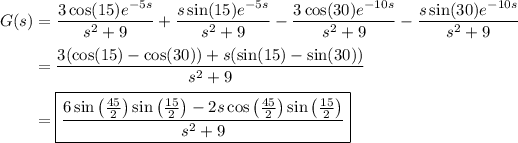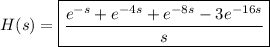This is made easy if you know the Laplace transform pair
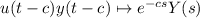
where u(t) is the Heaviside step function and Y(s) is the Laplace transform of y(t).
We rewrite f, g, and h in terms of u :
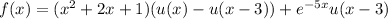
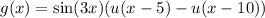
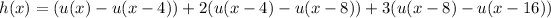
and we also rearrange terms to get the right shift in argument:
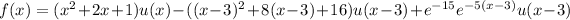
![g(x) = [\cos(15) \sin(3(x-5)) + \sin(15) \cos(3(x-5))] u(x-5) \\\\ ~~~~~~~~~~- [\cos(30) \sin(3(x-10)) + \sin(30) \cos(3(x-10))] u(x - 10)](https://img.qammunity.org/2023/formulas/mathematics/college/60gxqdyv4faeidxdrp6279c6scfi6ye4wx.png)
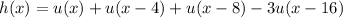
Now we can apply the known transform pair, along with
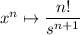

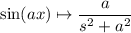
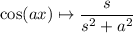
The transforms of f, g, and h are then