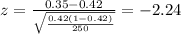Question

A publisher reports that 42%42% of their readers own a particular make of car. A marketing executive wants to test the claim that the percentage is actually different from the reported percentage. A random sample of 250250 found that 35%35% of the readers owned a particular make of car. Find the value of the test statistic. Round your answer to two decimal places.

Answer 1

`z=\frac{0.35 -0.42}{\sqrt{(0.42(1-0.42))/(250)}}=-2.24`

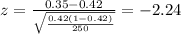
Explanation:

Data given and notation

n=250 represent the random sample taken

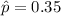`\hat p=0.35` estimated proportion of readers owned a particular make of car

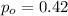`p_o=0.42` is the value that we want to test

z would represent the statistic (variable of interest)

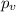`p_v` represent the p value (variable of interest)

Concepts and formulas to use

We need to conduct a hypothesis in order to test the claim that that the percentage is actually different from the reported percentage.:

Null hypothesis:
`p=0.42`

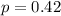
Alternative hypothesis:
`p \\eq 0.42`

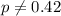
When we conduct a proportion test we need to use the z statistic, and the is given by:

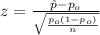`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

The One-Sample Proportion Test is used to assess whether a population proportion
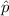`\hat p` is significantly different from a hypothesized value
`p_o`.

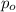Calculate the statistic

Since we have all the info requires we can replace in formula (1) like this:

`z=\frac{0.35 -0.42}{\sqrt{(0.42(1-0.42))/(250)}}=-2.24`