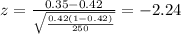Answer:
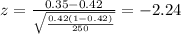
Explanation:
Data given and notation
n=250 represent the random sample taken
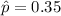 estimated proportion of readers owned a particular make of car
estimated proportion of readers owned a particular make of car
 is the value that we want to test
is the value that we want to test
z would represent the statistic (variable of interest)
 represent the p value (variable of interest)
represent the p value (variable of interest)
Concepts and formulas to use
We need to conduct a hypothesis in order to test the claim that that the percentage is actually different from the reported percentage.:
Null hypothesis:
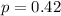
Alternative hypothesis:
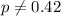
When we conduct a proportion test we need to use the z statistic, and the is given by:
 (1)
(1)
The One-Sample Proportion Test is used to assess whether a population proportion
 is significantly different from a hypothesized value
is significantly different from a hypothesized value
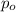 .
.
Calculate the statistic
Since we have all the info requires we can replace in formula (1) like this: