Question

The balanced combustion reaction for C 6 H 6 C6H6 is 2 C 6 H 6 ( l ) + 15 O 2 ( g ) ⟶ 12 CO 2 ( g ) + 6 H 2 O ( l ) + 6542 kJ 2C6H6(l)+15O2(g)⟶12CO2(g)+6H2O(l)+6542 kJ If 7.300 g C 6 H 6 7.300 g C6H6 is burned and the heat produced from the burning is added to 5691 g 5691 g of water at 21 ∘ 21 ∘ C, what is the final temperature of the water?

Answer 1

Answer: The final temperature of the water is
`33.85^(o)C`.

Step-by-step explanation:

We know that molar mass of
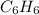`C_(6)H_(6)` is 78 g/mol. And, the amount of heat produced when 2 mol of
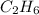`C_(2)H_(6)` burns is 6542 KJ.

This means that,

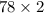`78 * 2` = 156 g of
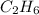`C_(2)H_(6)` burns, heat produced is 6542 kJ.

Therefore, heat produced (Q) by burning 7.3 g of
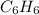`C_(6)H_(6)` is as follows.

`(6542 * 7.3 g)/(156 g)`

= 306.13 kJ

or, = 306130 J (as 1 KJ = 1000 J)

For water, mass is given as 5691 g and specific heat capacity of water is 4.186
`J/g^(o)C`.

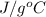So, we will calculate the value of final temperature as follows.

Q =
`m * C * (T_(f) - T_(i))`

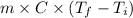
306130 J =
`5691 g * 4.186 J/g^(o)C * (T_(f) - 21)^(o)C`

`(T_(f) - 21)^(o)C = (306130 J)/(23822.53 J/^(o)C)`

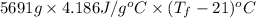
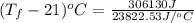
`T_(f)` = 12.85 + 21

=
`33.85^(o)C`

Thus, we can conclude that the final temperature of the water is
`33.85^(o)C`.