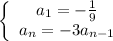Answer:
- r=3
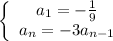
Explanation:
Given the sequence

The common ratio is determined by the division of term by the previous term.
Common Ratio,
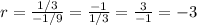
A recursive formula is a formula that defines each term of a sequence using preceding term(s).
For the given sequence, the recursive formula is: