Question

What is the volume of the right triangular prism shown?

Answer 1

Answer: 900 units cubed

Explanation:

Volume of right triangular prism is A=
`(bhl)/(2)` so plug in our known values...

A= (15x8x15)/2

A=1800/2

900

Answer 2

Given:

The sides of the base of the triangle are 8, 15 and 17.

The height of the prism is 15 units.

We need to determine the volume of the right triangular prism.

Area of the base of the triangle:

The area of the base of the triangle can be determined using the Heron's formula.

`S=(a+b+c)/(2)`

Substituting a = 8, b = 15 and c = 17. Thus, we have;

`S=(8+15+17)/(2)`

`S=(40)/(2)=20`

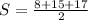
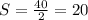
Using Heron's formula, we have;

`Area = √(S(S-a)(S-b)(S-c))`

`Area = √(20(20-8)(20-15)(20-17))`

`Area = √(20(12)(5)(3))`

`Area = √(3600)`

`Area = 36`

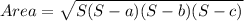
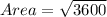
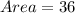
Thus, the area of the base of the right triangular prism is 36 square units.

Volume of the right triangular prism:

The volume of the right triangular prism can be determined using the formula,

`V=(1)/(2)A_b h`

where
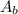`A_b` is the area of the base of the prism and h is the height of the prism.

Substituting the values, we have;

`V=(1)/(2)(60* 15)`

`V=450`

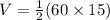
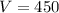
Thus, the volume of the right triangular prism is 450 cubic units.