Question

Triangle ABC is similar to Triangle FGH. What is the value of x in centimeters?

Answer 1

22.5

Explanation:

Answer 2

Given:

Given that the triangle ABC is similar to triangle FGH.

We need to determine the value of x.

Value of x:

Since, the triangles are similar, then their sides are proportional.

Thus, we have;

`(AC)/(FH)=(AB)/(GF)=(BC)/(GH)`

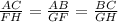
Let us consider the proportion
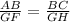`(AB)/(GF)=(BC)/(GH)` to determine the value of x.

Substituting AB = 9 cm, GF = 13.5 cm, BC = 15 cm and GH = x, we get;

`(9)/(13.5)=(15)/(x)`

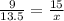
Cross multiplying, we get;

`9x=15 * 13.5`

`9x=202.5`

`x=22.5 \ cm`

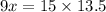
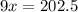
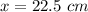
Thus, the value of x is 22.5 cm

Hence, Option F is the correct answer.