Given:
Given that the triangle ABC is similar to triangle FGH.
We need to determine the value of x.
Value of x:
Since, the triangles are similar, then their sides are proportional.
Thus, we have;
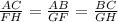
Let us consider the proportion
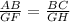 to determine the value of x.
to determine the value of x.
Substituting AB = 9 cm, GF = 13.5 cm, BC = 15 cm and GH = x, we get;
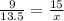
Cross multiplying, we get;
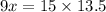
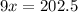
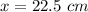
Thus, the value of x is 22.5 cm
Hence, Option F is the correct answer.