Answer:
Over the boundary: maximum:13, minimum:12
Over D: maximum:13, minimum:0
Explanation:
We are given that
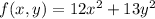 and D is the disc of radius one. Namely,
and D is the disc of radius one. Namely,
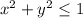 .
.
First, we want to find a critical point of the function f. To do so, we want to find the values(x,y) such that
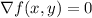 .
.
Recall that
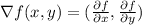 .
.
So, let us calculate
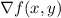 (the detailed calculation of the derivatives is beyond the scope of the answer.
(the detailed calculation of the derivatives is beyond the scope of the answer.
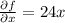

When equalling it to 0, we get that the critical point is (0,0), which is in our region D. Note that the function f is the sum of the square of two real numbers multiplied by some constants. Hence, the function f fulfills that
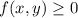 . Note that f(0,0)=0, so without further analysis we know that the point (0,0) is a minimum of f over D.
. Note that f(0,0)=0, so without further analysis we know that the point (0,0) is a minimum of f over D.
If we restrict to the boundary, we have the following equation
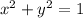 . Main idea is to replace the value of one of the variables n the function f, so it becomes a function of a single variable. Then, we can find the critical values by using differential calculus:
. Main idea is to replace the value of one of the variables n the function f, so it becomes a function of a single variable. Then, we can find the critical values by using differential calculus:
Case 1:
Let us replace y. So, we have that
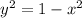 . So,
. So,
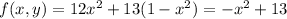 .
.
So, we will find the derivative with respect to x and find the critical values. That is
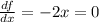
Which implies that x =0. Then,
 . So we have the following critical points (0,1), (0,-1). Notice that for both points, the value of f is f(0,1) = f(0,-1) = 13. If we calculate the second derivative, we have that at x=0
. So we have the following critical points (0,1), (0,-1). Notice that for both points, the value of f is f(0,1) = f(0,-1) = 13. If we calculate the second derivative, we have that at x=0
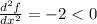 . By the second derivative criteria, we know that this points are local maximums of the function f.
. By the second derivative criteria, we know that this points are local maximums of the function f.
Case 2:
Let us replace x. So, we have that
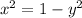 . So,
. So,
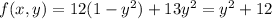 .
.
So, we will find the derivative with respect to y and find the critical values. That is
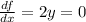
Which implies that y =0. Then,
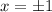 . So we have the following critical points (-1,0), (1,0). Notice that for both points, the value of f is f(1,0) = f(-1,0) = 12. If we calculate the second derivative, we have that at y=0
. So we have the following critical points (-1,0), (1,0). Notice that for both points, the value of f is f(1,0) = f(-1,0) = 12. If we calculate the second derivative, we have that at y=0
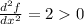 . By the second derivative criteria, we know that this points are local minimums of the function f.
. By the second derivative criteria, we know that this points are local minimums of the function f.
So, over the boundary D, the maximum value of f is 13 and the minimum value is 12. Over all D, the maximum value of f is 13 and the minimum value is 0.