Answer:
2195 MPa
Step-by-step explanation:
Given that:
Radius of curvature (
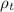 ) = 3 × 10⁻⁴ mm,
) = 3 × 10⁻⁴ mm,
Crack length (
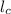 ) = 2.5 × 10⁻² mm,
) = 2.5 × 10⁻² mm,
Therefore the length of surface crack (a) = crack length / 2 = 2.5 × 10⁻² mm / 2 = 1.25 × 10⁻² mm,
Tensile stress (
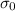 ) = 170 MPa = 170 × 10⁶ Pa
) = 170 MPa = 170 × 10⁶ Pa
The magnitude of the maximum stress that exists at the tip of an internal
crack (
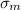 ) is given by the equation:
) is given by the equation:
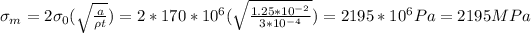
Therefore the maximum stress is 2195 MPa