Question

What is the magnitude of the maximum stress that exists at the tip of an internal crack having a radius of curvature of 3 × 10-4 mm (1.181 × 10-5 in.) and a crack length of 2.5 × 10-2 mm (0.9843 × 10-3 in.) when a tensile stress of 170 MPa (24660 psi) is applied?

Answer 1

2195 MPa

Step-by-step explanation:

Given that:

Radius of curvature (
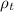`\rho_t`) = 3 × 10⁻⁴ mm,

Crack length (
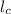`l_c`) = 2.5 × 10⁻² mm,

Therefore the length of surface crack (a) = crack length / 2 = 2.5 × 10⁻² mm / 2 = 1.25 × 10⁻² mm,

Tensile stress (
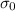`\sigma_0`) = 170 MPa = 170 × 10⁶ Pa

The magnitude of the maximum stress that exists at the tip of an internal

crack (
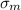`\sigma_m`) is given by the equation:

`\sigma_m=2\sigma_0(\sqrt{(a)/(\rho t) })=2* 170*10^6(\sqrt{(1.25*10^(-2))/(3*10^(-4)) } )=2195*10^6Pa=2195MPa`

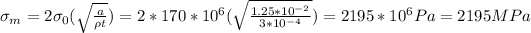
Therefore the maximum stress is 2195 MPa