Answer:
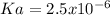
Step-by-step explanation:
Hello,
In this case, by knowing that in terms of the change
 due to the reaction extent, the percent dissociation is:
due to the reaction extent, the percent dissociation is:
![\% Dissociation:(x)/([acid]_0)](https://img.qammunity.org/2021/formulas/chemistry/college/xj6f5qu9ye4vh2y6g0l2mn2pzjnspfpv9f.png)
Thus, we compute
 as:
as:
![x=\% Dissociation*[acid]_0=0.89\%*0.031M=2.759x10^(-4)M](https://img.qammunity.org/2021/formulas/chemistry/college/qir46u2h73jbrxfwyuwhjjhs5nv6vfo5nx.png)
With that
 , we could assume the law of mass action for a typical dissociation:
, we could assume the law of mass action for a typical dissociation:
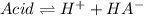
As:
![Ka=(x*x)/([acid]_0-x)=(2.759x10^(-4)M*2.759x10^(-4)M)/(0.031M-2.759x10^(-4)M) \\\\Ka=2.5x10^(-6)](https://img.qammunity.org/2021/formulas/chemistry/college/8rmfg5rf9bwlfrks2wkm8ifnk6f2al4j1p.png)
Best regards.