Question

a hollow shaft is required to transmit 600kw at 110 rpm, the maximum torque being 20% greater than the mean. the shear stress is not to exceed 63 mpa and twist in a length of 3 meters not t exeed 1.4 degrees Calculate the minimum external diameter satisfying these conditions.

Answer 1

175.5 mm

Step-by-step explanation:

a hollow shaft of diameter ratio 3/8 is required to transmit 600kw at 110 rpm, the maximum torque being 20% greater than the mean. the shear stress is not to exceed 63 mpa and twist in a length of 3 meters not t exeed 1.4 degrees Calculate the minimum external diameter satisfying these conditions. G = 80 GPa

Let

D = external diameter of shaft

Given that:

d = internal diameter of the shaft = 3/8 × D = 0.375D,

Power (P) = 600 Kw, Speed (N) = 110 rpm, Shear stress (τ) = 63 MPa = 63 × 10⁶ Pa, Angle of twist (θ) = 1.4⁰, length (l) = 3 m, G = 80 GPa = 80 × 10⁹ Pa

The torque (T) is given by the equation:

`T=(60 *P)/(2\pi N)\\ Substituting:\\T=(60*600*10^3)/(2\pi*110) =52087Nm`

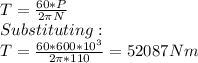
The maximum torque (
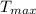`T_{max`) = 1.2T = 1.2 × 52087 =62504 Nm

Using Torsion equation:

`(T)/(J) =(\tau)/(R)\\ J=(T.R)/(\tau) \\(\pi)/(32)[D^4-(0.375D)^4]=(62504*D)/(2(63*10^6)) \\D^3(0.9473)=0.00505\\D=0.1727m=172.7mm`

`\theta=1.4^0=(1.4*\pi)/(180)rad`

From the torsion equation:

`(T)/(J) =(G\theta )/(l)\\ J=(T.l)/(G\theta) \\(\pi)/(32)[D^4-(0.375D)^4]=(62504*3)/(84*10^9*(1.4*\pi)/(180) ) \\D=0.1755m=175.5mm`

The conditions would be satisfied if the external diameter is 175.5 mm