Question

From a thin piece of cardboard 40 in. by 40 in., square corners are cut out so that the sides can be folded up to make a box. What dimensions will yield a box of maximum volume? What is the maximum volume? Round to the nearest tenth, if necessary.

Answer 1

The maximum dimension for box will be side length as 26.667 inches and height will be 6.667 inches and volume will be 4741 cu inches.

Explanation:

Given:

With dimensions as

40x40 square and sides are folded in square corners.

To Find:

Maximum volume that will yield and maximum dimension for box

Solution:

Consider, a box with 40 x 40 dimensions as follows and

let a x side length square corners are cut and folded up and a new figure is formed .and for that what will be the maximum volume and dimension.

Now,

as the there 2 corner for each side i.e. 2 square on side length

Resultant length will be 40-2x

So volume is given by ,

`V=l^2*h`

`=(40-2x)^2*x`

`V=(40^2-2*2x*40+4x^2)*x`

`V=(1600-160x+4x^2)*x`

`V=4x^3-160x^2+1600x`

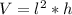
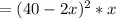
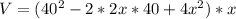
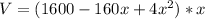
To get Maximum volume differentiate w.r.t 'x'

`V'=12x^2-320x+1600`

`V`

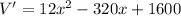
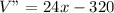
Now solve for x with help of quadratic equation we get ,

12x^2-320x+1600

=4(3x-20)(x-20)

Therefore ,

3x-20=0 or x-20=0

x=20/3 or x=20

x=16.666 or x=20

Now use this values in a 2nd derivative equation,

V"=24(6.667)-320)

V"=160-320

V"=-160 <0 ,................equation(1)[Here maximum volume will be presented]

For X=20

V"=24*20-320

V"=480-320

=160>0 ..................Equation(2)[here minimum volume will presented]

Comparing equation 1 and 2 we get ,

Take as x=20/3 as the folded square length as it is gives minimum value for 2nd derivative.

So

`V=(40-2x)^2*x`

`V=[40-2(20/3)]^2*20/3`

`V=[40-40/3]^2*6.667`

=
`[26.667]^2*6.667`

=4740.95

=
`4741 cu inches.`

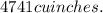
So side lengths =40-2x=40-2*20/3

=40(1-1/3)

=40(2/3)

=26.667 inches

And the height will be x=20/3=6.667 inches.