Question

A sample of 900900 computer chips revealed that 49%49% of the chips do not fail in the first 10001000 hours of their use. The company's promotional literature states that 52%52% of the chips do not fail in the first 10001000 hours of their use. The quality control manager wants to test the claim that the actual percentage that do not fail is different from the stated percentage. Determine the decision rule for rejecting the null hypothesis, H0H0, at the 0.020.02 level.

Answer 1

The proportion of chips that do not fail in the first 1000 hours of their use is 52%.

Explanation:

The claim made by the company is that 52% of the chips do not fail in the first 1000 hours of their use.

A quality control manager wants to test the claim.

A one-proportion z-test can be used to determine whether the proportion of chips do not fail in the first 1000 hours of their use is 52% or not.

The hypothesis can be defined as:

H₀: The proportion of chips do not fail in the first 1000 hours of their use is 52%, i.e. p = 0.52.

Hₐ: The proportion of chips do not fail in the first 1000 hours of their use is different from 52%, i.e. p ≠ 0.52.

The information provided is:

`\hat p=0.49\\n=900\\\alpha =0.02`

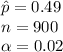
The test statistic value is:

`z=\frac{\hat p-p}{\sqrt{(p(1-p))/(n)}}=\frac{0.49-0.52}{\sqrt{(0.52(1-0.52))/(900)}}=-1.80`

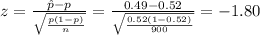
The test statistic value is -1.80.

Decision rule:

If the p-value of the test is less than the significance level then the null hypothesis will be rejected and vice-versa.

Compute the p-value as follows:

`p-value=2* P(Z<-1.80)\\=2* 0.03593\\=0.07186`

*Use a z-table.

The p-value = 0.07186 > α = 0.02.

The null hypothesis was failed to be rejected at 2% level of significance.

Conclusion:

The proportion of chips that do not fail in the first 1000 hours of their use is 52%.