Answer:
The proportion of chips that do not fail in the first 1000 hours of their use is 52%.
Explanation:
The claim made by the company is that 52% of the chips do not fail in the first 1000 hours of their use.
A quality control manager wants to test the claim.
A one-proportion z-test can be used to determine whether the proportion of chips do not fail in the first 1000 hours of their use is 52% or not.
The hypothesis can be defined as:
H₀: The proportion of chips do not fail in the first 1000 hours of their use is 52%, i.e. p = 0.52.
Hₐ: The proportion of chips do not fail in the first 1000 hours of their use is different from 52%, i.e. p ≠ 0.52.
The information provided is:
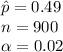
The test statistic value is:
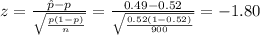
The test statistic value is -1.80.
Decision rule:
If the p-value of the test is less than the significance level then the null hypothesis will be rejected and vice-versa.
Compute the p-value as follows:
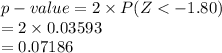
*Use a z-table.
The p-value = 0.07186 > α = 0.02.
The null hypothesis was failed to be rejected at 2% level of significance.
Conclusion:
The proportion of chips that do not fail in the first 1000 hours of their use is 52%.