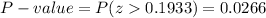Question

The mayor of a town has proposed a plan for the annexation of a new bridge. A political study took a sample of 900 voters in the town and found that 75% of the residents favored annexation. Using the data, a political strategist wants to test the claim that the percentage of residents who favor annexation is above 72%. Determine the P-value of the test statistic. Round your answer to four decimal places.

Answer 1

P-value of the test statistic: P=0.0266.

Explanation:

Hypothesis test on a proportion.

The claim is that the percentage of residents who favor annexation is above 72% This is going to be stated in the alternative hypothesis.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.72\\\\H_a:\pi>0.72`

The sample size is n=900 and the sample proportion is p=0.75.

The standard devaition is calculated as:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.72*0.28)/(900)}=√(0.000224)=0.015`

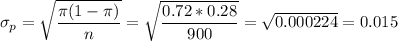
Then, the z-statistic is:

`z=(p-\pi-0.5/n)/(\sigma_p)=(0.75-0.72-0.5/900)/(0.015)=(0.029)/(0.015) = 1.9333`

For this right tailed test, the P-value is:

`P-value=P(z>0.1933)=0.0266`