Answer:
Check step-by-step-explanation.
Explanation:
A given criteria for geometric series of the form
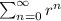 is that
is that
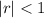 . Other wise, the series diverges. When it converges, we know that
. Other wise, the series diverges. When it converges, we know that
 .
.
So,
a)
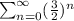 diverges since
diverges since
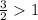
b)
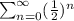 converges since
converges since
 , and
, and
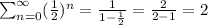
c)We can use the series in b) but starting at n=1 instead of n=0. Since they differ only on one term, we know it also converges and
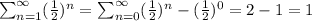 .
.
d)Based on point c, we can easily generalize that if we consider the following difference
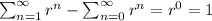
So, they differ only by 1 if the series converges.