Answer:
Slope of the line that is parallel: -5
Slope of the line that is perpendicular:
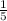
Explanation:
For the parallel line:
Rewrite your equation to slope-intercept form: y = mx + b
y = mx + b
- m = slope
- b = y-intercept (when x = 0)
-5x - y = 1 <== add 5x to both sides
+5x +5x
-y = 5x + 1 <== divide both sides by -1
/-1 /-1
y = -5x - 1
The slope of the line that is parallel to this line is -5.
For the perpendicular line:
*Perpendicular lines have negative reciprocals*
Steps:
1. Take your original slope (-5)
2. Flip it (-1/5)
3. Change the sign (1/5)
For a slope of -5, the reciprocal would be:
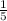
Hope this helps!