Question

Find the slope of the line that is parallel and perpendicular to the following equation.

-5x - y = 1

Answer 1

Slope of the line that is parallel: -5

Slope of the line that is perpendicular:
`(1)/(5)`

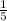
Explanation:

For the parallel line:

Rewrite your equation to slope-intercept form: y = mx + b

y = mx + b

• m = slope
• b = y-intercept (when x = 0)

-5x - y = 1 <== add 5x to both sides

+5x +5x

-y = 5x + 1 <== divide both sides by -1

/-1 /-1

y = -5x - 1

The slope of the line that is parallel to this line is -5.

For the perpendicular line:

*Perpendicular lines have negative reciprocals*

Steps:

1. Take your original slope (-5)

2. Flip it (-1/5)

3. Change the sign (1/5)

For a slope of -5, the reciprocal would be:
`(1)/(5)`

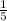
Hope this helps!

Answer 2

slope of perpendicular:
`\sf \bold{(1)/(5) }}`

slope of parallel: -5

rewrite in slope intercept form: [ y = mx + b ]

• -5x - y = 1

• -y = 1 + 5x

• y = -5x - 1

comparing with y = mx + b [ where m is slope, b is y-intercept ]

Parallel slope is same

formula: m₁ = m₂

• m = -5

slope of parallel: -5

Perpendicular slope is negatively reciprocal

formula: m₁ = -(m₂)⁻¹

• m₁ = -(-5)⁻¹

• m₁ = -(-1/5)

• m₁ = 1/5

slope of perpendicular: 1/5