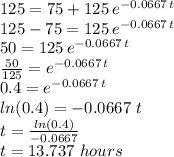Question

In a certain power plant it was found necessary to store some water in a vertical tank 5 inches in diameter and 10 ft. long at a temperature of 200 degrees F. When the water temperature dropped to 125 degrees F it was necessary to replenish the tank with hot water. Observations showed that it cooled 10 degrees F in 1 hour 15 minutes at an outside temperature of 75 degrees F. How long will it take to cool to 125 degrees F when the 100 drop in 1.25 hours occurs with the initial water temperature of 2000 F.

Answer 1

It takes approximately 13.737 hours for the 200 degree water to cool down to 125 degrees.

Explanation:

Recall Newton's Law of heating and cooling for an object of initial temperature
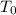`T_0`, in an ambient temperature
`T_a`:

`T(t)=T_a+(T_0-T_a)\,e^(-kt)`

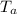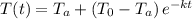
where t is the time elapsed.

We know the ambient temperature and the initial temperature of the object, but we don't know the value of the constant "k" that describes the cooling process. We can obtain such value (k) by using the information that the 200 degrees water cooled 10 degrees in 1.25 hours.

In such case we have:

`T(t)=T_a+(T_0-T_a)\,e^(-kt)\\200-10=75+(200-75)\,e^(-k(1.25))\\190=75+125\,e^(-k(1.25))\\190-75=125\,e^(-k(1.25))\\115=125\,e^(-k(1.25))\\(115)/(125)= e^(-k(1.25))\\0.92=e^(-k(1.25))\\ln(0.92)=-k\,(1.25)\\k=(ln(0.92))/(-1.25) \\k=0.0667`

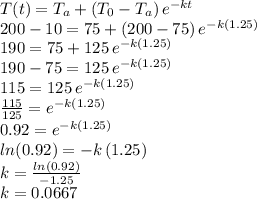
Therefore, we have now the complete expression for the cooling process:

`T(t)=75+125\,e^(-0.0667\,t)`

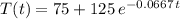
To find the time it takes to cool the 200 degree water down to 125 degrees, we use:

`125=75+125\,e^(-0.0667\,t)\\125-75=125\,e^(-0.0667\,t)\\50=125\,e^(-0.0667\,t)\\(50)/(125) =e^(-0.0667\,t)\\0.4=e^(-0.0667\,t)\\ln(0.4)=-0.0667\,\,t\\t=(ln(0.4))/(-0.0667) \\t=13.737\,\,hours`