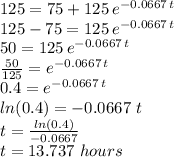Answer:
It takes approximately 13.737 hours for the 200 degree water to cool down to 125 degrees.
Explanation:
Recall Newton's Law of heating and cooling for an object of initial temperature
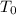 , in an ambient temperature
, in an ambient temperature
 :
:
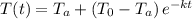
where t is the time elapsed.
We know the ambient temperature and the initial temperature of the object, but we don't know the value of the constant "k" that describes the cooling process. We can obtain such value (k) by using the information that the 200 degrees water cooled 10 degrees in 1.25 hours.
In such case we have:
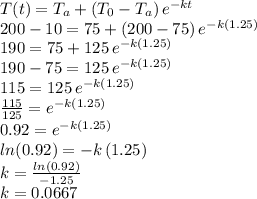
Therefore, we have now the complete expression for the cooling process:
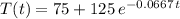
To find the time it takes to cool the 200 degree water down to 125 degrees, we use: