Answer: We do not sufficient evidence that mean is greater than 0.
Explanation:
Since we have given that
n = 36
mean = 0.9
Standard deviation = 15.8
at 0.01 level of significance,
Hypothesis would be:
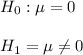
Standard error of mean would be :
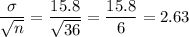
statistic value would be :
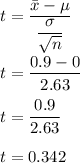
Degree of freedom = df = 36-1=35
So, p value = 2.4377
Since 2.4377 > 0.342, we will not reject null hypothesis.
Hence, We do not sufficient evidence that mean is greater than 0.