Question

Find the slope of the line that is parallel and perpendicular to the following equation.

y + 4 = -3(x +1)

Answer 1

Parallel: -3

Perpendicular: 1/3

Step-by-step explanation:

First I would convert the equation into slope-intercept form to more easily identify the slope:

`y+4=-3x-3\\ y=-3x-7`

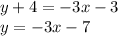
Slope-intercept form is defined as y=mx+b where m is the slope and b is the y-intercept so we can identify the slope of this line as -3.

When a line is parallel to another line, this means that they have the same slope, therefore the slope of the line parallel to the equation is -3.

Perpendicular lines will have slopes that are negative reciprocals of each other, the negative reciprocal of -3 is 1/3; therefore, the slope of the line perpindicular to the equation is 1/3.

Answer 2

parallel slope = -3

perpendicular slope:
`\sf \bold{(1)/(3) }`

Step-by-step explanation:

• y + 4 = -3(x +1)

• y + 4 = -3(x) - 3

• y = -3(x) - 3 - 4

• y = -3x - 7

comparing with y = m(x) + b [ "m" is the slope, "b" is the y-intercept ]

• slope: -3

• y-intercept: -7

Parallel/Tangent slope:

m₁ = m₂ (same)

Perpendicular/Normal slope:

m₁ * m₂ = -1 (negatively reciprocal)

⇒ Here parallel slope:

• m = -3

⇒ Here perpendicular slope:

• -3 * m₂ = -1

• m₂ = -1/-3

• m₂ = 1/3