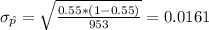Answer:

The mean is given by:
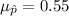
And the deviation:
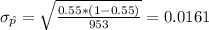
Explanation:
For this case we assume that the true population proportion of Americans do not know that GOP stands for Grand Old Party is 0.55 and we select a random sample of n = 953 americans
For this case we assume that we satisfy the conditions to use the normal approximation for

1) np >10 , n(1-p)>10
2) Independence
3) Random sample
4) The sample size is less than 10% of the population size
We assume that all the conditions are satisfied and the distribution for
 would be:
would be:

The mean is given by:
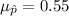
And the deviation: