Question

Cousin Throckmorton is playing with the clothesline. One end of the clothesline is attached to a vertical post. Throcky holds the other end loosely in his hand, so that the speed of waves on the clothesline is a relatively slow 0.740m/s . He finds several frequencies at which he can oscillate his end of the clothesline so that a light clothespin 43.0cm from the post doesn't move. What are these frequencies?

Answer 1

Frequencies are 0.86Hz

Step-by-step explanation:

Given v=0.74m/s

d= 0.43m

Lambda/2=0.43m

Thus lambda= 0.86m

And F= v/lambda

0.74/0.86= 0.86Hz

Answer 2

The obsrved frquencies are
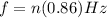`f= n (0.86) Hz` n = 1,2,3,...,n.

Step-by-step explanation:

From the question we are told that

The speed of the wave is v = 0.740 m/s

The distance from the post is
`d = 43.0cm = (43)/(10) = 0.43m`

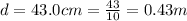
Generally frequency is mathematically represented as

`f = (v)/(\lambda )`

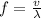
so for the first frequency which the the fundamental frequency(first harmonic frequency) the clothesline(string) would form only one loop and hence the length between the vertical post and throcky hands is mathematically represented as

`L = (\lambda)/(2)`

=>
`\lambda = 2L`

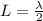
So

`f_f =f_1= (v)/(2L)`

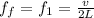
Substituting values

`f_f = f_1 = (0.740)/(2* 0.43)`

`= 0.860 Hz`

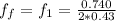
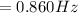
For the second harmonic frequency i.e is when the clothesline(string) forms two loops the length is mathematically represented as

`L = \lambda`

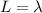
So the second harmonic frequency is

`f_2 = (v)/(L)`

`f_2 = 2 * (v)/(2L)`

`f_2 =(0.740)/(0.430)`

`= 1.72Hz`

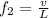
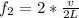
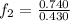
For the third harmonic frequency i.e when the clothesline(string) forms three loops the length is mathematically represented as

`L = 3 * (\lambda )/(2)`

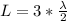
So the wavelength is

`\lambda = (2L)/(3)`

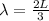
And the third harmonic frequency is mathematically evaluated as

`f_3 = (v)/((2L)/(3) )`

`= 3 * (v)/(2L)`

`f_3=2.58Hz`

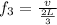
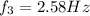
Looking at the above calculation we can conclude that the harmonic frequency of a vibrating string(clothesline) can be mathematically represented as an integer multiple of the fundamental frequency

i.e

`f = n f_f`

`f = n (v)/(2L)`

`f= n (0.86) Hz`

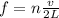
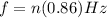
Where n denotes integer values i.e n = 1,2,3,....,n.

Note : The length that exist between two nodes which are successive is equivalent to half of the wavelength so when one loop is form the number of nodes would be 2 and on anti-node