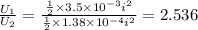Answer:
Ratio of energy stored in the inductor will be 2.536
Step-by-step explanation:
We have given two inductance
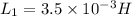
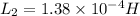
As inductors are connected in series so current will be same in both inductor
Energy stored in inductor is equal to
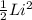
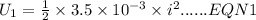
Energy stored in second inductor
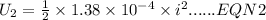
Dividing equation 1 by equation 2