Question

A nuclear power plant based on the Rankine cycle operates with a boiling-water reactor to develop net cycle power of 3 MW. Steam exits the reactor core at 100 bar, 620°C and expands through the turbine to the condenser pressure of 1 bar. Saturated liquid exits the condenser and is pumped to the reactor pressure of 100 bar. Isentropic efficiencies of the turbine and pump are 87% and 78%, respectively. Cooling water enters the condenser at 15°C with a mass flow rate of 114.79 kg/s. Determine: (a) the percent thermal efficiency. (b) the temperature of the cooling water exiting the condenser, in °C.\

Answer 1

(a) The percentage thermal efficiency is approximately 30.54%

(b) The temperature of the cooling water exiting the condenser is approximately 28 °C

Step-by-step explanation:

In the question, we note that the boiler is the rector, therefore

T₁ = 620 °C = ‪893.15 K

P₁ = 100 bar

(a) From super heated steam tables at 100 bar, 600 °C

S₆₀₀ = 6.9045 kJ·kg⁻¹·K⁻¹

S₆₅₀ = 7.0409 kJ·kg⁻¹·K⁻¹

By interpolation, we have S₆₂₀ given by

`S_(620) = S_(600) + (S_(650) - S_(600))(620 - 600)/(650 - 600)`

`S_(620) = 6.9045 + (7.0409 - 6.9045 )(620 - 600)/(650 - 600)`

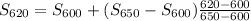
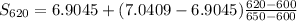
S₆₂₀ = 6.95906 kJ·kg⁻¹·K⁻¹

Therefore, S₁ = S₆₂₀ = 6.95906 kJ·kg⁻¹·K⁻¹

Similarly

h₆₀₀ = 3625.84 kJ·kg⁻¹

h₆₅₀ = 3748.32 kJ·kg⁻¹

`h_(620) = 3625.84 + (3748.32 - 3625.84 )(620 - 600)/(650 - 600)`

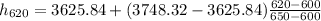
h₆₂₀ = 3674.832 kJ·kg⁻¹

h₁ = h₆₂₀ = 3674.832 kJ·kg⁻¹

Therefore, T₂ is given by

T₂ = Temperature at 1 bar = 99.6059 °C = ‪372.7559 K

At S₁ = S₂ we have

S'₂ at 1 bar = 1.3026 kJ·kg⁻¹·K⁻¹

S''₂ at 1 bar = 7.3588 kJ·kg⁻¹·K⁻¹

Therefore, steam fraction x₂ is given by;

S₁ = S'₂ + (S''₂ - S'₂)×x₁

6.95906 =1.3026 + (7.3588 - 1.3026)×x₁

x₂ = 0.93399 ≈ 0.934

From which, h₂ = 417.436 + (2674.95 - 417.436)×0.934 = 2,524.94 kJ·kg⁻¹

Where saturated liquid exits the condenser, we have

h₃ = 417.436 kJ·kg⁻¹ it

`v = v_f \ at 1 \ bar`

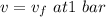
v = 0.00104315 = m³·kg⁻¹

Work done by pump =
`v_f * (p_4 - p_3)`

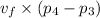
∴ Work done by pump = 0.00104315 × (‪10000000 - ‪100000) = 10431.395685 J/kg = 10.431 kJ/kg

Therefore, h₄ - h₃ = 10.431 kJ/kg

The percent the thermal efficiency of the cycle is then

`Cycle \ efficiency = ((h_1-h_2)-(h_4-h_3))/(Gross\ heat \ supplied)`

`Cycle \ efficiency = ((h_1-h_2)-(h_4-h_3))/((h_1-h_3)-(h_4-h_3))`

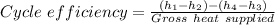
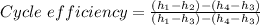
Where the turbine efficiency = 87% and the condenser efficiency = 78% we have

`Cycle \ efficiency = ((h_1-h_2) * 0.87-(h_4-h_3) * 0.78)/((h_1-h_3)-(h_4-h_3) * 0.78)`

`Cycle \ efficiency = ((3674.832 -2,524.94 )-10.431)/(Gross\ heat \ supplied)`

`Cycle \ efficiency = (1149.892 * 0.87-10.431 * 0.78)/((3674.832 -417.436 )-10.431 * 0.78) = 0.305383`

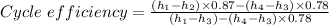
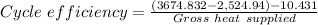
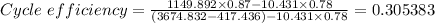
Therefore the cycle efficiency as a percentage = 0.305383 × 100 = 30.5383% ≈ 30.54%

(b) The temperature of the cooling water exiting the condenser is given by

Heat rejected in condenser = Heat absorbed by the cooling water

Heat rejected in condenser = -Q₂₃ = h₂ - h₃

∴ Heat rejected in condenser, -Q₂₃ = 2,524.94 kJ·kg⁻¹ - 417.436 kJ·kg⁻¹

∴ -Q₂₃ = 2107.504 kJ·kg⁻¹

Net cycle power = -∑ = W₁₂ - W₃₄ = 1149.892×0.87 - 10.431×0.78

Net cycle power = 1008.54222 kJ/s = 1.008542 MW

Where the developed net cycle power = 3 MW

The mass is given by 3/1.008542 = 2.975 kg

∴ Heat absorbed by the cooling water = 2107.504 kJ·kg⁻¹ × 2.975 kg

Heat absorbed by the cooling water = 6268.9612 kJ

Mass flow rate of cooling water = 114.79 kg/s

Therefore, from ΔQ = m·c·ΔT we have

Heat absorbed by 114.79 kg/s of cooling water = 6268.9612 kJ

Specific heat capacity of water = 4.2 kJ/kg

Therefore

6268.9612 kJ = 4.2×114.79×(T₂ - 15 °C)

∴T₂ = 15°C + 6268.9612 /(4.2×114.79) = 28.003 °C ≈ 28 °C.