Answer:
(a) The percentage thermal efficiency is approximately 30.54%
(b) The temperature of the cooling water exiting the condenser is approximately 28 °C
Step-by-step explanation:
In the question, we note that the boiler is the rector, therefore
T₁ = 620 °C = 893.15 K
P₁ = 100 bar
(a) From super heated steam tables at 100 bar, 600 °C
S₆₀₀ = 6.9045 kJ·kg⁻¹·K⁻¹
S₆₅₀ = 7.0409 kJ·kg⁻¹·K⁻¹
By interpolation, we have S₆₂₀ given by
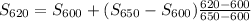
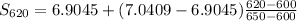
S₆₂₀ = 6.95906 kJ·kg⁻¹·K⁻¹
Therefore, S₁ = S₆₂₀ = 6.95906 kJ·kg⁻¹·K⁻¹
Similarly
h₆₀₀ = 3625.84 kJ·kg⁻¹
h₆₅₀ = 3748.32 kJ·kg⁻¹
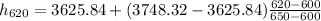
h₆₂₀ = 3674.832 kJ·kg⁻¹
h₁ = h₆₂₀ = 3674.832 kJ·kg⁻¹
Therefore, T₂ is given by
T₂ = Temperature at 1 bar = 99.6059 °C = 372.7559 K
At S₁ = S₂ we have
S'₂ at 1 bar = 1.3026 kJ·kg⁻¹·K⁻¹
S''₂ at 1 bar = 7.3588 kJ·kg⁻¹·K⁻¹
Therefore, steam fraction x₂ is given by;
S₁ = S'₂ + (S''₂ - S'₂)×x₁
6.95906 =1.3026 + (7.3588 - 1.3026)×x₁
x₂ = 0.93399 ≈ 0.934
From which, h₂ = 417.436 + (2674.95 - 417.436)×0.934 = 2,524.94 kJ·kg⁻¹
Where saturated liquid exits the condenser, we have
h₃ = 417.436 kJ·kg⁻¹ it
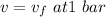
v = 0.00104315 = m³·kg⁻¹
Work done by pump =
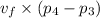
∴ Work done by pump = 0.00104315 × (10000000 - 100000) = 10431.395685 J/kg = 10.431 kJ/kg
Therefore, h₄ - h₃ = 10.431 kJ/kg
The percent the thermal efficiency of the cycle is then
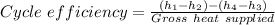

Where the turbine efficiency = 87% and the condenser efficiency = 78% we have
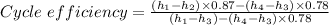
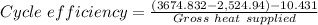
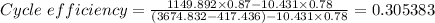
Therefore the cycle efficiency as a percentage = 0.305383 × 100 = 30.5383% ≈ 30.54%
(b) The temperature of the cooling water exiting the condenser is given by
Heat rejected in condenser = Heat absorbed by the cooling water
Heat rejected in condenser = -Q₂₃ = h₂ - h₃
∴ Heat rejected in condenser, -Q₂₃ = 2,524.94 kJ·kg⁻¹ - 417.436 kJ·kg⁻¹
∴ -Q₂₃ = 2107.504 kJ·kg⁻¹
Net cycle power = -∑ = W₁₂ - W₃₄ = 1149.892×0.87 - 10.431×0.78
Net cycle power = 1008.54222 kJ/s = 1.008542 MW
Where the developed net cycle power = 3 MW
The mass is given by 3/1.008542 = 2.975 kg
∴ Heat absorbed by the cooling water = 2107.504 kJ·kg⁻¹ × 2.975 kg
Heat absorbed by the cooling water = 6268.9612 kJ
Mass flow rate of cooling water = 114.79 kg/s
Therefore, from ΔQ = m·c·ΔT we have
Heat absorbed by 114.79 kg/s of cooling water = 6268.9612 kJ
Specific heat capacity of water = 4.2 kJ/kg
Therefore
6268.9612 kJ = 4.2×114.79×(T₂ - 15 °C)
∴T₂ = 15°C + 6268.9612 /(4.2×114.79) = 28.003 °C ≈ 28 °C.