Answer:
The change in temperature of the lead bullet is 333.06 ⁰C
Step-by-step explanation:
Given;
mass of the lead bullet , m = 3.5 g = 0.0035 kg
velocity of the bullet, v = 292 m/s
specific heat capacity of the lead bullet, c = 128 J/kg.◦ C
let Δθ = change is temperature
Kinetic energy of the bullet is calculated using the formula below;
K.E = ¹/₂mv²
K.E = ¹/₂(0.0035)(292)²
K.E = 149.212 J
If all the kinetic energy of the lead bullet is converted to thermal energy and none leaves the bullet, then the temperature change is calculated using the formula below;
K.E = Q
where;
Q is the quantity of heat generated by the moving bullet or say heat capacity of the lead bullet
Q = mcΔθ
where;
m is mass of the bullet
c is specific heat capacity of the lead bullet
Δθ is the change in temperature
Δθ
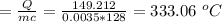
Therefore, the change in temperature of the lead bullet is 333.06 ⁰C