Answer:
The upper limit is 10.1
The lower limit is 9.91
Step-by-step explanation:
Given that:
The mean fill level (μ) = 10.01 ounces,
Standard deviation (σ) = 0.25 ounces
Number of sample bottles (n) = 20
The limits of the sample mean = 92% = 0.92
α = 1 - 0.92 = 0.08

The z value of 0.04 is the same as the z value of 0.46 (0.5 - 0.04). From the probability distribution table:
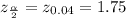
The margin of error (e) is given by:
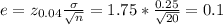
The upper limit = μ + e = 10.01 + 0.1= 10.1
The lower limit = 10.01 - 0.1 = 9.91