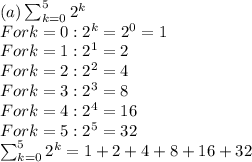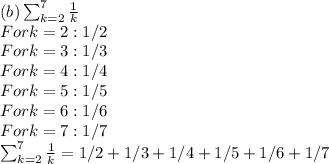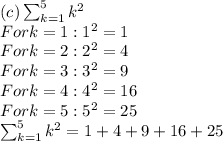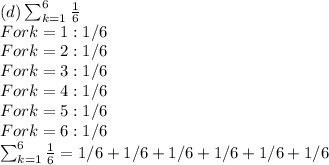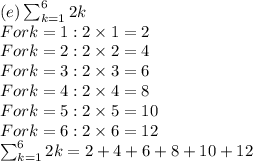The correct question is:
Write out the following sums, one term for each value of k. Simplify each term as much as possible, but do not enter decimals. For example, enter 1 + 4 + 9 instead of 1² + 2² + 3² or 14, or enter 1/2 + 1/2 instead of 0.5 + 0.5 or 1.
The purpose of this problem is for you to show that you know how to interpret summation notation and write all of the terms in a sum, which is why you are being told not to reduce your answers very much.
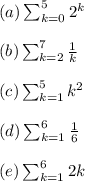
Answer:
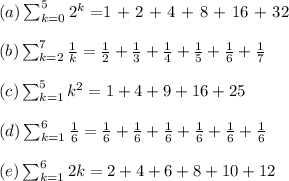
Explanation: