Question

An incoming college student took her college’s placement exams in French and mathematics. In French, she scored 85, and in math 80. The overall results for both exams are approximately normal. The mean French test score was 72 with a SD of 12, while the mean math test score was 68 with a SD of 8. On which exam did she do better as compared with the other incoming college students? Compute the z-scores and the percentiles for each exam to support your answer

Answer 1

In Math, she scored in the 93rd percentile, which is higher than the French percentile. So she did better on the Math exam as compared with the other incoming college students

Explanation:

Z-score:

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

On which exam did she do better as compared with the other incoming college students?

On the exam for which she had the higher z-score.

Franch:

Scored 85.

Mean 72, SD = 12. So

`Z = (X - \mu)/(\sigma)`

`Z = (85 - 72)/(12)`

`Z = 1.08`

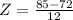
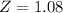
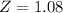`Z = 1.08` has a pvalue of 0.8810, so her French score is in the 88th percentile.

Math:

Scored 80

Mean 68, SD = 8. So

`Z = (X - \mu)/(\sigma)`

`Z = (80 - 68)/(8)`

`Z = 1.5`

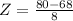
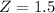
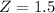`Z = 1.5` has a pvalue of 0.9332.

In Math, she scored in the 93rd percentile, which is higher than the French percentile. So she did better on the Math exam as compared with the other incoming college students