Question

For which values of k would the product of k/3 X 12 be greater than 12

Answer 1

`\text{k = 4, 5, 6, 7, 8... and onwards}`

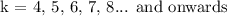
Explanation:

The product of k/3 and 12 be greater than 12.

⇒ k/3 × 12 > 12

The first step in determining the possible values of "k" is to simplify the left-hand-side (L.H.S) of the inequality.

⇒ (12 × k)/3 > 12

⇒ (12 ÷ 3) × k > 12

⇒ (4) × k > 12

The next step in determining the possible values of "k" is to isolate the variable. To do this, we can divide 4 both sides.

⇒ [4 × k]/4 > 12/4

⇒ k > 12/4

⇒ k > 3

To satisfy the inequality, the value of k must be greater than 3. Thus, the values of k could be
`\text{4, 5, 6... }` and so on.