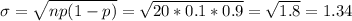Question

Bill Connors, a quality control manager at a Menlo Park Electronics Company, knows his company has been making surge protectors with a 10% rate of defective units. Bill decides to test 20 randomly selected surge protectors to see how many are defective. Let X represent the mumber f defective unit nth . Asminnpndenc answer the folowing :a) What type of probability distribution does X have (include the value(s) of any parameters)? b) What is the probability that more than one surge protector is defective? c) What is the probability that the number of defective surge protectors is between three and five? d) How many surge protectors would you expect to be defective? e) Find the standard deviation X.

Answer 1

a) Binomial distribution, with n=20 and p=0.10.

b) P(x>1) = 0.6082

c) P(3≤X≤5) = 0.3118

d) E(X) = 2

e) σ=1.34

Explanation:

a) As we have a constant "defective" rate for each unit, and we take a random sample of fixed size, the appropiate distribution to model this variable X is the binomial distribution.

The parameters of the binomial distribution for X are n=20 and p=0.10.

`X\sim B(0.10,20)`

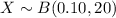
b) The probability of k defective surge protectors is calculated as:

`P(x=k) = \binom{n}{k} p^(k)q^(n-k)`

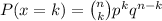
In this case, we want to know the probability that more than one unit is defective: P(x>1). This can be calculated as:

`P(x>1)=1-(P(0)+P(1))\\\\\\P(x=0) = \binom{20}{0} p^(0)q^(20)=1*1*0.1216=0.1216\\\\P(x=1) = \binom{20}{1} p^(1)q^(19)=20*0.1*0.1351=0.2702\\\\\\ P(x>1)=1-(0.1216+0.2702)=1-0.3918=0.6082`

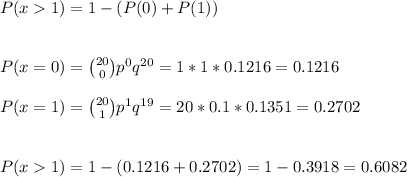
c) We have to calculate the probability that the number of defective surge protectors is between three and five: P(3≤X≤5).

`P(3\leq X\leq 5)=P(3)+P(4)+P(5)\\\\\\P(x=3) = \binom{20}{3} p^(3)q^(17)=1140*0.001*0.1668=0.1901\\\\P(x=4) = \binom{20}{4} p^(4)q^(16)=4845*0.0001*0.1853=0.0898\\\\P(x=5) = \binom{20}{5} p^(5)q^(15)=15504*0*0.2059=0.0319\\\\\\P(3\leq X\leq 5)=P(3)+P(4)+P(5)=0.1901+0.0898+0.0319=0.3118`

d) The expected number of defective surge protectors can be calculated from the mean of the binomial distribution:

`E(X)=\mu_B=np=20*0.10=2`

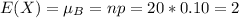
e) The standard deviation of this binomial distribution is:

`\sigma=√(np(1-p))=√(20*0.1*0.9)=√(1.8)=1.34`