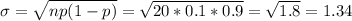Answer:
a) Binomial distribution, with n=20 and p=0.10.
b) P(x>1) = 0.6082
c) P(3≤X≤5) = 0.3118
d) E(X) = 2
e) σ=1.34
Explanation:
a) As we have a constant "defective" rate for each unit, and we take a random sample of fixed size, the appropiate distribution to model this variable X is the binomial distribution.
The parameters of the binomial distribution for X are n=20 and p=0.10.

b) The probability of k defective surge protectors is calculated as:
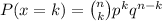
In this case, we want to know the probability that more than one unit is defective: P(x>1). This can be calculated as:
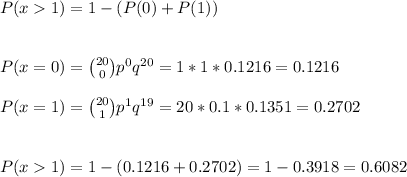
c) We have to calculate the probability that the number of defective surge protectors is between three and five: P(3≤X≤5).

d) The expected number of defective surge protectors can be calculated from the mean of the binomial distribution:
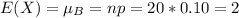
e) The standard deviation of this binomial distribution is: