Question

For the given maximization​ problem, (a) determine the number of slack variables​ needed, (b) name​ them, and​ (c) use slack variables to convert each constraint into a linear equation. a. How many slack variables are​ needed? 3 b. Which slack variables should be​ used? A. s 1​, s 2​, s 3 B. s 1​, s 2 C. x 1​, x 2​, x 3 D. x 1​, x 2 c. What is the equation using a slack variable that corresponds to the first​ constraint, 5 x 1 plus 8 x 2 plus 10 x 3 less than or equals 173​? A. 5 x 1 plus 8 x 2 plus 10 x 3 less than or equals 173 B. 5 x 1 plus 8 x 2 plus 10 x 3 plus s 1 less than or equals 173 C. 5 x 1 plus 8 x 2 plus 10 x 3 plus x 1 equals 173 D. 5 x 1 plus 8 x 2 plus 10 x 3 plus s 1 equals 173 What is the equation using a slack variable that corresponds to the second​ constraint, 5 x 1 plus 4 x 2 plus 17 x 3 less than or equals 245​? A. 5 x 1 plus 4 x 2 plus 17 x 3 plus s 2 equals 245 B. 5 x 1 plus 4 x 2 plus 17 x 3 less than or equals 245 C. 5 x 1 plus 4 x 2 plus 17 x 3 plus x 2 equals 245 D. 5 x 1 plus 4 x 2 plus 17 x 3 plus s 2 less than or equals 245 Maximize zequals5x 1plus3x 2plusx 3 subject​ to: 5 x 1 plus 8 x 2 plus 10 x 3 less than or equals 173 5 x 1 plus 4 x 2 plus 17 x 3 less than or equals 245 with x 1greater than or equals​0, x 2greater than or equals​0, x 3greater than or equals0

Answer 1

A. Two slack variables are needed

B. S1 and s2 (option b)

C. Option d (5X1 + 8X2 + 10X3 + s1 = 173)

D. Option a (5X1 + 4X2 + 17X3 + s2 = 245)

E. Z is maximized at 173 when (X1, X2, X3) = (34.6, 0, 0)

Explanation:

In a linear maximization problem like this, if we want to convert the inequality (constraint) into a linear equation, we add slack variables to the left hand side of each inequality.

Therefore we add s1 and s2 to the first and second inequality respectively.

`5X1 + 8X2 + 10X3 \leq 173\\5X1 + 4X2 + 17X3 \leq 245`

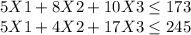
Imputing the slack variables, we obtain as follows:

`5X1 + 8X2 + 10X3 + s1 = 173\\5X1 + 4X2 + 17X3 + s2 = 245`

`Maximize :\\Z = 5X1 + 3X2 + X3`

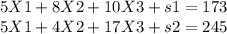
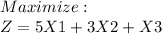
Subject to

`5X1 + 8X2 + 10X3 \leq 173\\5X1 + 4X2 + 17X3 \leq 245\\With \\X1 \geq 0\\X2 \geq 0\\X3 > 0`

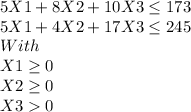
Solution :

`5X1 + 8X2 + 10X3 + s1 = 173\\5X1 + 4X2 + 17X3 + s2 = 245\\-5X1 - 3X2 - X3 + Z = 0`

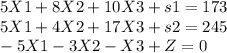
5X1 on the first equation is the pivot because the negative value of -5 is the highest and 173/5 is less than 245/5

We perform eq1 - eq2 on the first row and eq1 + eq3 on the third row to get X1 and clear the rest.

We

X1 = 173/5 = 34.6

X2 = 0 (inactive)

X3 = 0 (inactive)

s1 = 0 , s2 = -72/-1 = 72,

Z = 173/1 =173

Therefore the minimum value of Z is 173 when (X1, X2, X3) = (34.6, 0, 0)

Answer 2

a) 2

b) s₁ and s₂

c) First linear equation: 5*x₁ + 8*x₂ + 10*x₃ + s₁ = 173

Second linear equation: 5*x₁ + 4*x₂ + 17*x₃ + s₂ = 254

Explanation:

The problem statement, establishes two constraints, each one of them will need a slack variable to become a linear equation, so the answer for question

a) 2.

b) The constraints are: s₁ and s₂

c) First constraint

5*x₁ + 8*x₂ + 10*x₃ ≤ 173

We add slack variable s₁ and the inequality becomes

5*x₁ + 8*x₂ + 10*x₃ + s₁ = 173

The second constraint is:

5*x₁ + 4*x₂ + 17*x₃ ≤ 254

We add slack variable s₂ and the inequality becomes

5*x₁ + 4*x₂ + 17*x₃ + s₂ = 254