Answer:
Δπ Min = -0.0709
Δπ Max = -0.0535
Explanation:
Here we have

Where:
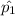 = 13% = 0.13
= 13% = 0.13
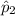 = 14% = 0.14
= 14% = 0.14
n₁ = 163
n₂ = 160
Therefore, we have;
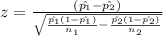
Plugging the values gives
z = -0.263
CI 90% = critical z =
 1.644
1.644
The minimum difference in true proportion = -0.0709
The maximum difference in true proportion = 0.0535.