Question

A reservation service employs six information operators who receive requests for information independently of one another, each according to a Poisson process with rate ???? = 2 per minute. a. What is the probability that during a given 1 min period, the first operator receives no requests? (Round your answer to three decimal places.) b. What is the probability that during a given 1 min period, exactly three of the six operators receive no requests? (Round your answer to five decimal places.)

Answer 1

a) 0.135 = 13.5% probability that during a given 1 min period, the first operator receives no requests.

b) 0.03185 = 3.185% probability that during a given 1 min period, exactly three of the six operators receive no requests

Explanation:

To solve this question, we need to understand the Poisson distribution and the binomial distribution.

Poisson distribution:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

Binomial distribution:

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

Poisson process with rate 2 per minute

This means that
`\mu = 2`

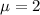
a. What is the probability that during a given 1 min period, the first operator receives no requests?

Single operator, so we use the Poisson distribution.

This is P(X = 0).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-2)*2^(0))/((0)!) = 0.135`

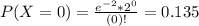
0.135 = 13.5% probability that during a given 1 min period, the first operator receives no requests.

b. What is the probability that during a given 1 min period, exactly three of the six operators receive no requests?

6 operators, so we use the binomial distribution with
`n = 6`

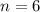
Each operator has a 13.5% probability of receiving no requests during a minute, so
`p = 0.135`

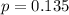
This is P(X = 3).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 3) = C_(6,3).(0.135)^(3).(0.865)^(3) = 0.03185`

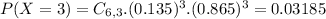
0.03185 = 3.185% probability that during a given 1 min period, exactly three of the six operators receive no requests