Question

A box is being created out of a 15 inch by 10 inch sheet of metal. Equal-sized squares are cutout of the corners, then the sides are folded up to create an open-top box. What size squaresshould be cut out so that the box has the largest possible volume?

Answer 1

Therefore the dimensions of the square should be 0.1528 inch by 0.1528 inch so, the box has largest volume.

Explanation:

Given that,

A box is being created out of a 15 inches by 10 inches sheet of metal.

The length of the one side of the squares which are cut out of the each corners of the metal sheet be x.

The length of the metal box be = (15-2x) inches.

The width of the metal box be =(10-2x) inches

The height of the metal box be =x inches

Then, the volume of the metal box= length×width×height

=(15-2x)(10-2x)x cubic inches

=(150x-50x²+4x³) cubic inches

∴ V= 4x³-50x²+15x

Differentiating with respect to x

V'=12x²-100x+15

Again differentiating with respect to x

V''=24x-100

For maximum or minimum value, V'=0

12x²-100x+15=0

Apply quadratic formula
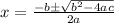`x=(-b\pm√(b^2-4ac))/(2a)`, here a=12, b= -100 and c=15

`x=(-(-100)\pm√((-100)^2-4.12.15))/(2.12)`

`\Rightarrow x=(100\pm√(9280))/(2.12)`

`\Rightarrow x=0.1528,8.18`

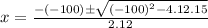
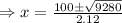
For x= 8.18, The value of (15-2x) and (10-2x) will negative.

∴x=0.1528 .

Now,
`V''|_(x=0.1528)=24(0.1528)-100<0`

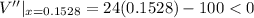
∴At x=0.1528 inch, the volume of the metal box will be maximum.

Therefore the dimensions of the square should be 0.1528 inch by 0.1528 inch so, the box has largest volume.