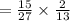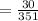Question

There are 27 chocolates in a box, all identically shaped. There 4 are filled with nuts, 8 with caramel, and 15 are solid chocolate. You randomly select one piece, eat it, and then select a second piece. Find the probability of selecting a solid chocolate candy followed by a nut candy.

Answer 1

Therefore the required probability is
`(30)/(351)`.

Explanation:

Two events are dependents event if the occurrence of one of them has effect on the probability of the other.

If A and B are dependents,

then,

P(AB)=P(A)P(B).

Given that,

There are 27 chocolates in a box.

Number of nuts chocolates = 4

Number of caramel chocolates = 8

Number of solid chocolates= 15.

The probability of that a solid candy is drawn is

`=\frac{\textrm{Number of solid chocolate}}{\textrm{Total number of chocolate}}`

`=(15)/(27)`.

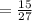After selecting a solid chocolate, the number of chocolate is= (27-1)=26.

The probability that a nut candy is drawn is

`=\frac{\textrm{Number of nut chocolate}}{\textrm{Total number of chocolate}}`

`=(4)/(26)`

`=(2)/(13)`

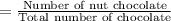
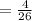
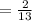
Therefore the required probability is

`=(15)/(27)*(2)/(13)`

`=(30)/(351)`