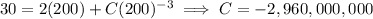Question

a tank contains 200 liters of fluid in which 30 grams of salt is dissolved. Brine containing 2 grams of salt per liter is then pumped into the tank at a rate of 4 L/min. The well-mixed solution is pumped out at a slower rate of 3 L/min. Write a differential equation that models the amount of salt in the tank at any time.

Answer 1

Salt flows in at a rate of

(2 g/L) * (4 L/min) = 8 g/min

and out at a rate of

(B/(200 + t) g/L) * (3 L/min) = 3B/(200 + t) g/min

where B is the amount of salt in the tank at time t.

Then the net rate at which B changes is governed by the ODE,

`B'=8-(3B)/(200+t)`

`B'+(3B)/(200+t)=8`

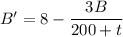
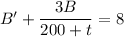
Multipy both sides by
`(200+t)^3`:

`(200+t)^3B'+3B(200+t)^2=8(200+t)^3`

`\left(B(200+t)^3\right)'=8(200+t)^3`

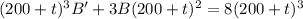
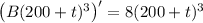
Integrate both sides:

`B(200+t)^3=2(200+t)^4+C`

`B=2(200+t)+C(200+t)^(-3)=(2(200+t)^4+C)/((200+t)^3)`

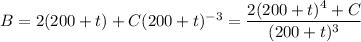
The tank starts with 30 g of salt, so B(0) = 30, which gives

`30=2(200) + C(200)^(-3)\implies C=-2,960,000,000`